(210912) Review-随机优化_首页-新宝GG娱乐-注册站

行业资讯

(210912) Review-随机优化

回顾一阶与二阶优化技术后，针对前者进行展开，涉及的主要是一阶梯度法；常见的一阶梯度法包括 SGD、Momentum、Nesterov、AdaGrad、RMSProp、Adam等等。其中SGD、Momentum、Nesterov是手动指定学习率的，而 AdaGrad、RMSProp、Adam 能够自动调节学习率。

这些算法又可以称之为 Stochastic Optimization（随机优化），优化的过程中引入了物理学的概念“动量”，通过一阶动量与二阶动量的刻画来更新学习率进而寻找到最优点；此处提及的优化算法都遵循一定的优化算法框架，针对其中的“动量”环节不断迭代和提升。

本次 Review 课程先给出常见的优化算法框架，再针对 SGD、AdaGrad、RMSprop、Adam进行展开。

一般用一个通用框架来表述优化算法，有如下定义：

待优化的参数 $\ heta$
目标函数 $J(\ heta)$
学习率 $\\alpha$

有如下过程（每次迭代）：

计算目标关于此时参数的梯度 $? θ ( J ( θ ) )$
计算历史梯度的一阶动量和二阶动量
计算下降梯度 $g$
根据梯度进行迭代 $θ=θ ? \\alpha g$

优化算法目前有固定学习率和自适应学习率，两种的差别体现在过程的第1和第2步。

固定学习率优化算法有：BGD、SGD、Mini-Batch GD
自适应学习率优化算法有：Adam、AdaGrad、AdaDelta

补充一下，动量梯度下降（Gradient Descent With Momentum），简称为动量方法（Momentum），运行速度几乎总是快于标准的梯度下降算法，并且能够解决随机梯度下降所遇到的山谷震荡以及鞍部停滞问题，更多关于“动量”可移步：深度学习中的Momentum算法原理[1]、模型优化-动量方法[2]。

现在用的最多的算法是 SGD 和 Adam，两者各有好坏。相对而言，SGD 能够到达全局最优解，而且训练的最佳精度也要高于其他优化算法，但它对学习率的调节要求非常严格，而且容易停在鞍点；Adam很容易的跳过鞍点，而且不需要人为的干预学习率的调节，但是它很容易在局部最小值处震荡，存在在特殊的数据集下出现学习率突然上升，造成不收敛的情况。

关于两者有很多相关的问题，可移步问题：SGD和Adam优化器的区别是什么？

【推荐阅读】

关于优化算法框架，Juliuszh：一个框架看懂优化算法之异同 SGD/AdaGrad/Adam
使用频率最高的优化算法，SGD有多种改进的形式(RMSprop,Adadelta等),为什么大多数论文中仍然用SGD?
关于Lecture中提到的二阶优化方法的实际使用，神经网络的训练可以采用二阶优化方法吗（如 Newton、Quasi Newton）？

BGD: batch gradient descent
SGD: stochastic gradient descent

梯度下降 (Gradient Decent) 是优化算法的一种，其思想是让损失函数沿着梯度的方向下降，以最快的速度取到最小值。为什么是沿梯度的方向？因为梯度 (gradient) 就是函数变化最快的方向[3]。

批量梯度下降（BGD）是梯度下降最基本的形式，它需要遍历所有的训练样本，这将带来庞大的计算量，在样本数量巨大的情况下会更为明显。

为了避免这个问题引入了随机梯度下降（SGD），SGD 是为了避免 BGD 在样本数量大时带来的巨大计算量；巨大的计算量来自每次迭代对整个训练集的遍历，所以 SGD 每次更新只选择一个样本。

AdaGrad 可以自动变更学习率：设定一个全局的学习率，但这并非是实际学习速率；实际的学习率是与以往参数的模之和的开方成反比的。

AdaGrad 能够实现学习率的自动更改：若梯度大，那么学习率衰减快一些（激励阶段）；若梯度小，那么学习率衰减慢一些（惩罚阶段）。对于每个参数，随着其更新的总距离增多，其学习速率也随之变慢。经验表明，AdaGrad 在普通算法中效果不错，但在深度学习中深度过深时会造成训练提前结束。

为了进一步优化损失函数在更新中存在摆动幅度过大的问题，并且进一步加快函数的收敛，于是提出了 RMSprop，该算法通过引入一个衰减系数，让梯度累计量 $r$ 每回合都衰减一定比例，类似于 Momentum 中的做法，是对 AdaGrad 算法的改进。

RMSprop 的优点是减小了梯度在变化幅度较大的分量上的更新速度，提高了变化幅度较小的分量上的更新速度，使用了指数移动加权平均来对历史梯度信息做处理，提高了收敛速度。RMSprop 可以实现学习率自适应调整，变化较大的梯度分量上的学习率会自动减小，变化较小的梯度分量上的学习率会自动增大。

RMSprop 的缺点是依然依赖于全局学习率。它是 Adagrad 的一种发展，和 Adadelta 的变体，效果趋于二者之间；适合处理非平稳目标，针对 RNN 效果不错。

Adam 算法和传统的随机梯度下降不同。随机梯度下降保持单一的学习率 $\\alpha$ 更新所有的权重，学习率在训练过程中并不会改变；而 Adam 通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。

以上提到的优化算法分为最基本的优化算法、自适应参数的优化算法两类，后者较前者最大的区别是每个参数有不同的学习率，在整个学习过程中自动适应这些学习率。

【最基本的优化算法】

SGD（随机梯度下降法）：SGD 实际就是 min-batch 的实现，为最基础的优化算法，当今大部分优化算法都是以SGD为基础实现的；
Momentum（动量法）：Momentum引入了动量 v，以指数衰减的形式累计历史梯度，以此来解决 Hessian 矩阵病态问题；
Nesterov（牛顿动量）：上文中没有具体提及 Nesterov，但它是 Momentum 的变种；与Momentum不同的是，Nesterov先更新参数，再计算梯度；

【自适应参数的优化算法】

AdaGrad：学习率逐参数的除以历史梯度平方和的平方根，使得每个参数的学习率不同；
RMSprop：AdaGrad算法的改进，历史梯度平方和—>指数衰减的移动平均，以此丢弃遥远的过去历史；
Adam：可以看做是修正后的 Momentum + RMSprop 算法；

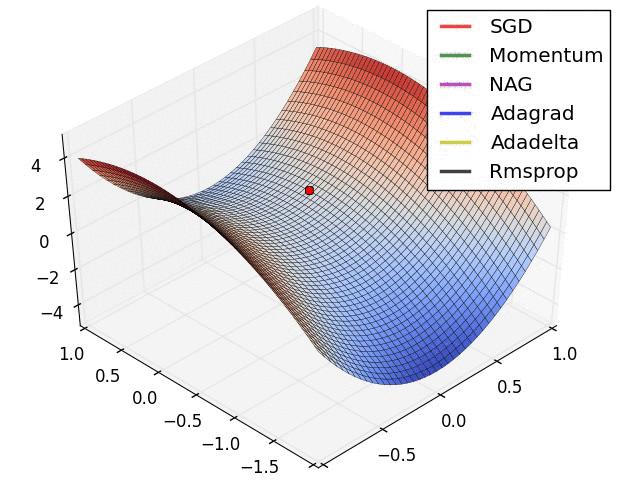
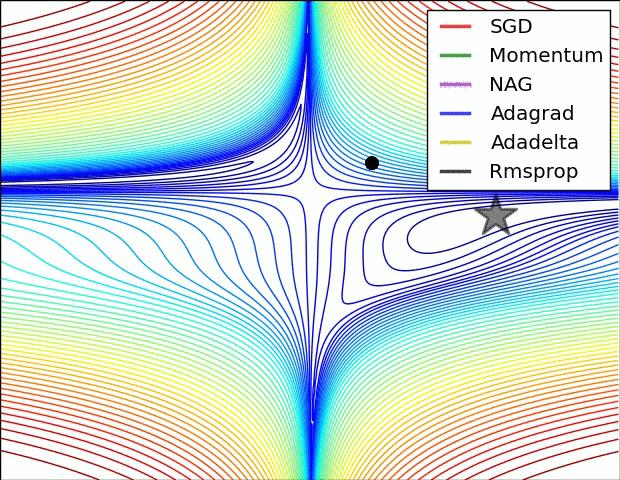
以下是算法描述，详细可移步：Deep Learning 之最优化方法[4]，这里有一个关于优化算法的动态示意图理解，具体可移步：梯度下降方法的视觉解释（动量，AdaGrad，RMSProp，Adam）[5]。

【推荐阅读】

[1]. Paul-LangJun. (2020). 深度学习中的Momentum算法原理. CSDN: https://blog.csdn.net/gaoxueyi551/article/details/105238182
[2]. clvsit. (2019). 模型优化-动量方法. CSDN: https://blog.csdn.net/weixin_43378396/article/details/90741645
[3]. Zero黑羽枫. (2019). 梯度下降总结(BGD ,SGD, MBGD). CSDN: 梯度下降总结(BGD ,SGD, MBGD)
[4]. BVL10101111. (2017). Deep Learning 之最优化方法. CSDN: https://blog.csdn.net/BVL10101111/article/details/72614711
[5]. taotao_2016. (2020). 梯度下降方法的视觉解释（动量，AdaGrad，RMSProp，Adam）. 360个人图书馆: http://www.360doc.com/content/20/0611/01/32196507_917690415.shtml

上一篇: 什么是真-假-处理过——宝石优化处理详解

下一篇: 新加坡最值得去参观的旅游景点是什么？

[返回列表]